03. Doppler Estimation
Header Text
Doppler Estimation
L2A12 Doppler Estimation
Doppler Estimation Overview
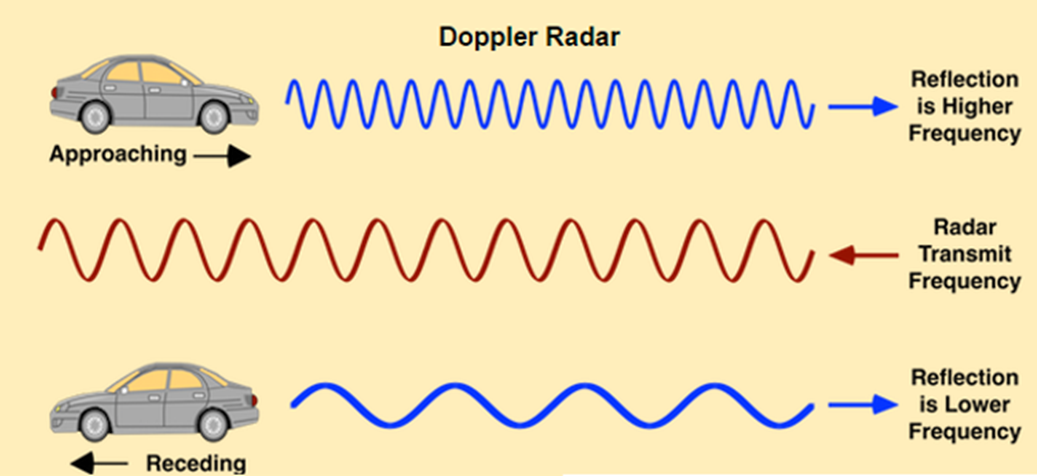
Doppler Speed Measurement
Doppler Estimation Theory
The velocity estimation for radar is based on an age old phenomenon called the doppler effect. As per doppler theory an approaching target will shift an emitted and reflected frequency higher, whereas a receding target will shift the both frequencies to be lower than the transmitted frequency.
The same principle is used in the radar guns to catch the speed violators, or even in sports to measure the speed of a ball.

ND313 Andrei Intv 15 What Is The Doppler Effect
FMCW Doppler Measurements
FMCW Doppler Measurements
FMCW Doppler Estimation
source : Delft University of Technology
As discussed above, there will be a shift in the received signal frequency due to the doppler effect of the target’s velocity. The doppler shift is directly proportional to the velocity of the target as shown below.
- f_D : shift in the transmitted frequency due to the doppler
- \nu_r : relative velocity of the target
- \lambda : wavelength of the signal
By measuring the shift in the frequency due to doppler, radar can determine the velocity. The receding target will have a negative velocity due to the frequency dropping lower, whereas the approaching target will have positive velocity as the frequency shifts higher.
The beat frequency comprises of both frequency components: f_r (frequency delta due to range) and f_d (frequency shift due to velocity). Although, in the case of automotive radar the f_d is very small in comparison to the f_r . Hence, the doppler velocity is calculated by measuring the rate of change of phase across multiple chirps.
The following equation shows the relationship between the rate of change of the phase \Phi , and the frequency:
DOPPLER PHASE SHIFT
Keeping that in consideration, we calculate the doppler frequency by measuring the rate of change of phase. The phase change occurs due to small displacement of a moving target for every chirp duration. Since, each chirp duration is generally in microseconds, it results in small displacement in mm (millimeters). These small displacements for every chirp leads to change in phase. Using this rate of change of phase we can determine the doppler frequency.
Let's see how :
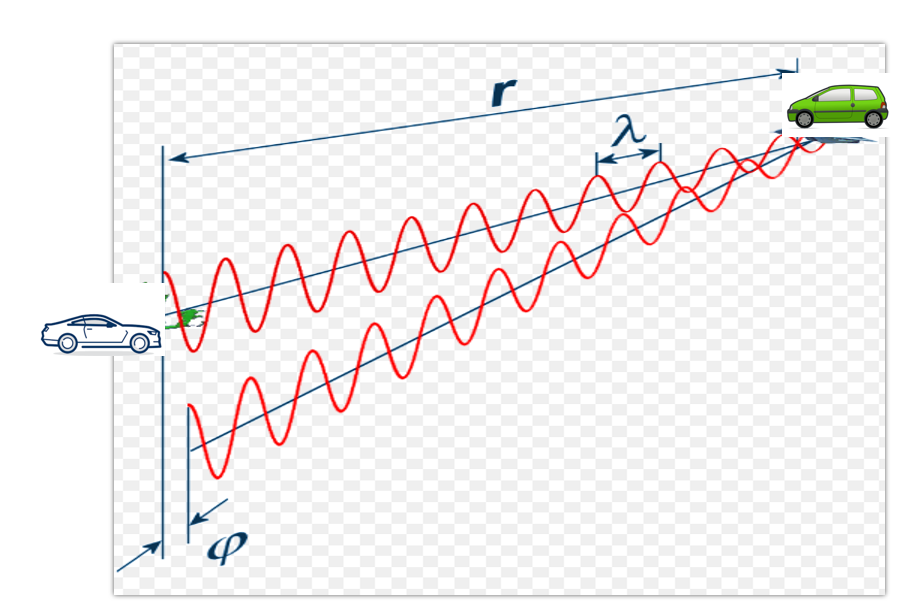
If the path between a target and the radar is changed by an amount Δx, the phase of the wave received by radar is shifted by
where λ and f are, respectively, the wavelength and frequency of the signal and c is the speed of propagation. The resulting change in observed frequency is
where Δt is the time taken for the observation of the phase change.
Doppler Estimation Exercises
Using the following MATLAB code sample, complete the TODOs to calculate thevelocity in m/s of four targets with following doppler frequency shifts: [3 KHz, 4.5 KHz, 11 KHz, -3 KHz].
You can use the following parameter values:
- The radar's operating frequency = 77 GHz
- The speed of light c = 3*10^8
% Doppler Velocity Calculation
c = 3*10^8; %speed of light
frequency = 77e9; %frequency in Hz
% TODO : Calculate the wavelength
% TODO : Define the doppler shifts in Hz using the information from above
% TODO : Calculate the velocity of the targets fd = 2*vr/lambda
% TODO: Display resultsDoppler Velocity
SOLUTION:
Target CDoppler Velocity 2
SOLUTION:
Target BSolution
3 Doppler Velocity
Doppler Estimation Further Research
Doppler Estimation Further Research
For additional resources related to doppler estimation, see these lecture notes .